| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- C
- 수치해석
- 백준 C#
- 입출력
- 백준 9465
- 철자검사
- dp
- 파라메트릭 서치
- 확률
- BFS
- 프로그래머스 c#
- 백준
- 통계
- 코딩테스트
- 선형대수학
- 문자열
- horner
- 통계학
- 너비우선탐색
- 알고리즘
- C#
- cpp
- horner algorithm
- 프로그래머스
- C++
- 프로그래머스C#
- 이분탐색
- 확률론
- 스티커 C++
- 9095 C++
- Today
- Total
HOIT_B
확률변수의 기댓값과 분산 본문
이산형 분포의 기댓값
x : 이산형 확률변수
f(x) : 확률 함수
∑|x|f(x) < ∞ 이면 'x는 기댓값이 존재한다'라고 하고 E(x) = ∑|x|f(x) 를 x의 기댓값이라 한다.
(ex)

연속형 분포의 기댓값
x : 연속 확률변수
f(x) : 확률함수
∫|x|f(x) dx <∞ 이면 'x는 기댓값이 존재한다'라고 하고 E(x) = ∫|x|f(x) dx를
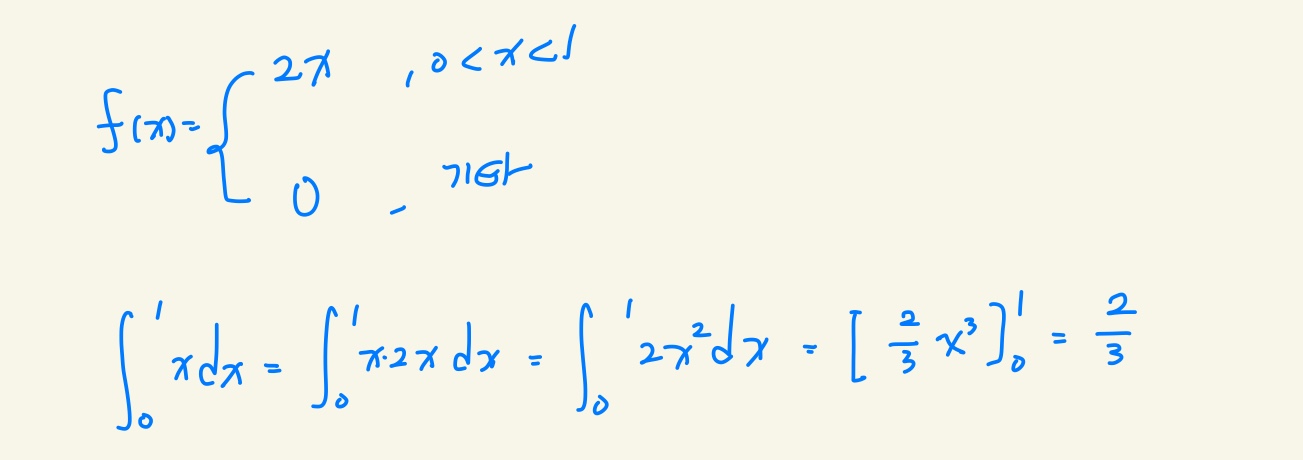
기댓값의 성질
확률변수 x는 E(x)가 존재할 때, 모든 a, b는 상수

THM
확률변수 X1, X2가 서로 독립이면 E( X1, X2 ) = E(X1) E(X2)이다.
(증명)

분산
확률변수 x는 E(x)=m를 가질 때, E[ (x-m)^2 ]이 존재하면 이 값을 x의 분산이라 한다.
var(x), v(x) 등으로 표기한다.
분산의 성질
모든a,b는 상수
var(ax+b) = a^2 var(x)
pf) var(ax+b) = E[ { (ax+b) - E(ax+b)^2 }^2 ] = E[ {ax+b - aE(x)+b}^2 ] = E[ { a(x-E(x) }^2 ] = a^2E[ { x-E(x) }^2 ]=a^2 var(x)
var(x+b) = var(x)
var(-x) = var(x)
THM
1) var(x) = E(x^2) - [E(x)]^2
(pf)

2) 확률변수 x1,x2가 서로 독립이면 var(x1+x2) = var(x1)+var(x2) 이다.
n으로 확장하면 x1, x2, x3, .......... ,xn이 서로 독립이면, var(x1+x2+x3+ ..........+xn) = var(x1)+var(x2)+var(x3) + ...... +var(xn)
(pf)


