| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 확률
- 통계학
- BFS
- cpp
- horner algorithm
- 백준
- 선형대수학
- C
- dp
- 철자검사
- 백준 9465
- 알고리즘
- 통계
- 이분탐색
- C#
- horner
- 문자열
- 확률론
- 백준 C#
- 코딩테스트
- 파라메트릭 서치
- 입출력
- 너비우선탐색
- 9095 C++
- 프로그래머스
- C++
- 수치해석
- 스티커 C++
- 프로그래머스C#
- 프로그래머스 c#
- Today
- Total
HOIT_B
다변량 분포 본문
다변량 분포 : 확률 실험에서 어떤 사건이 두 개 이상의 확률변수들에 의해 표현되는 경우
(ex) 신체조건 -> 키, 몸무게
체력검사 -> 달리기, 공던지기, 매달리기
두 개 이상의 확률변수들의 결합 확률 분포를 다변량 분포라고 한다. 특히, 2개의 확률변수의 결합 확률 분포를 이변량 분포라고 한다.
이변량 확률변수 : S : sample space , 모든 s∈S
두 개의 확률변수 X, Y에 대해서 X=X(s) , Y= Y(s)라 할 때 (X, Y)를 2 변량 확률변수라고 한다.
이때, X(s) = x, Y(s) = y , x, y∈실수 이면 (X, Y)를 2 변량 이산 확률변수라고 하고
X(s)∈I1(구간), Y(s)∈I2(구간) 이면 (X, Y)를 2 변량 연속 확률변수라고 한다.
이변량 이산형 결합 분포
2 변량 이산 확률변수 (X, Y)가 각각 X1, X2,....... Y1, Y2........ 의 값을 취할 때 (Xi , Yi)에 그의 확률 P(Xi, Yi) = P(X=xi, Y=yi)를 대응시키는 관계를 X, Y의 이산형 결합 확률분포라 하고 이때 f(x, y)=P(xi, yi)를 X, Y의 결합 확률 함수라 한다.
결합 확률 함수의 성질
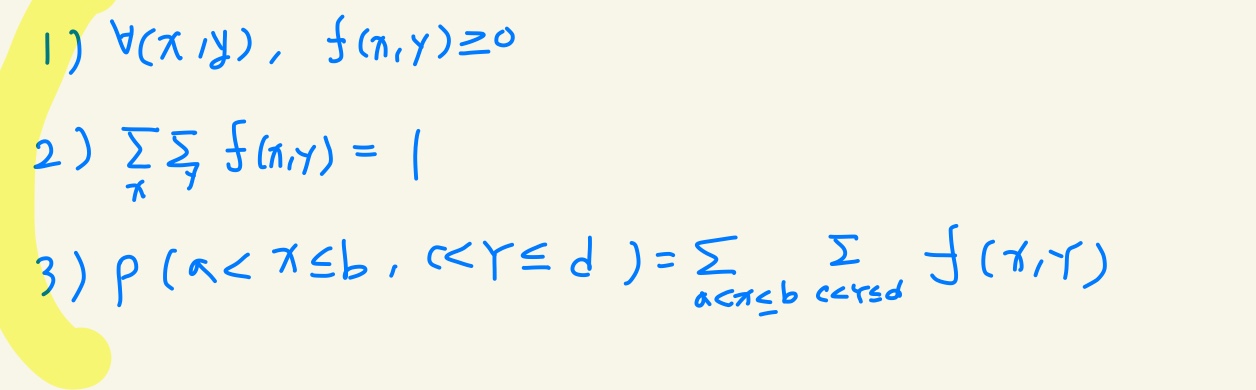
이변량 이산형 결합 분포 예 동전을 3번 던지는 실험
확률변수 X : 두 번째 던졌을 때까지의 앞면의 개수
확률변수 Y : 세 번째 던졌을 때까지의 앞면의 개수

이변량 연속형 결합 분포
2 변량 연속 확률변수(X, Y)가 취하는 값 (x, y)가 어떤 영역 A에 속하는 확률을 P(A)라고 할 때, P(A) = ∬f(x, y) dxdy로 나타내는 f(x, y)가 존재하면 확률변수 (X, Y)는 연속형 결합 확률분포를 가진다고 하고 이때 f(x, y)를 결합 확률 밀도 합수라고 한다.
결합 확률 밀도 함수의 성질

결합 확률 밀도 함수의 예
한 점 (X, Y)를 원 x^2 + y^2 ≤ 1의 내부 S로부터 무작위로 뽑을 때(뽑힐 확률은 일정) 결합 확률 밀도 함수
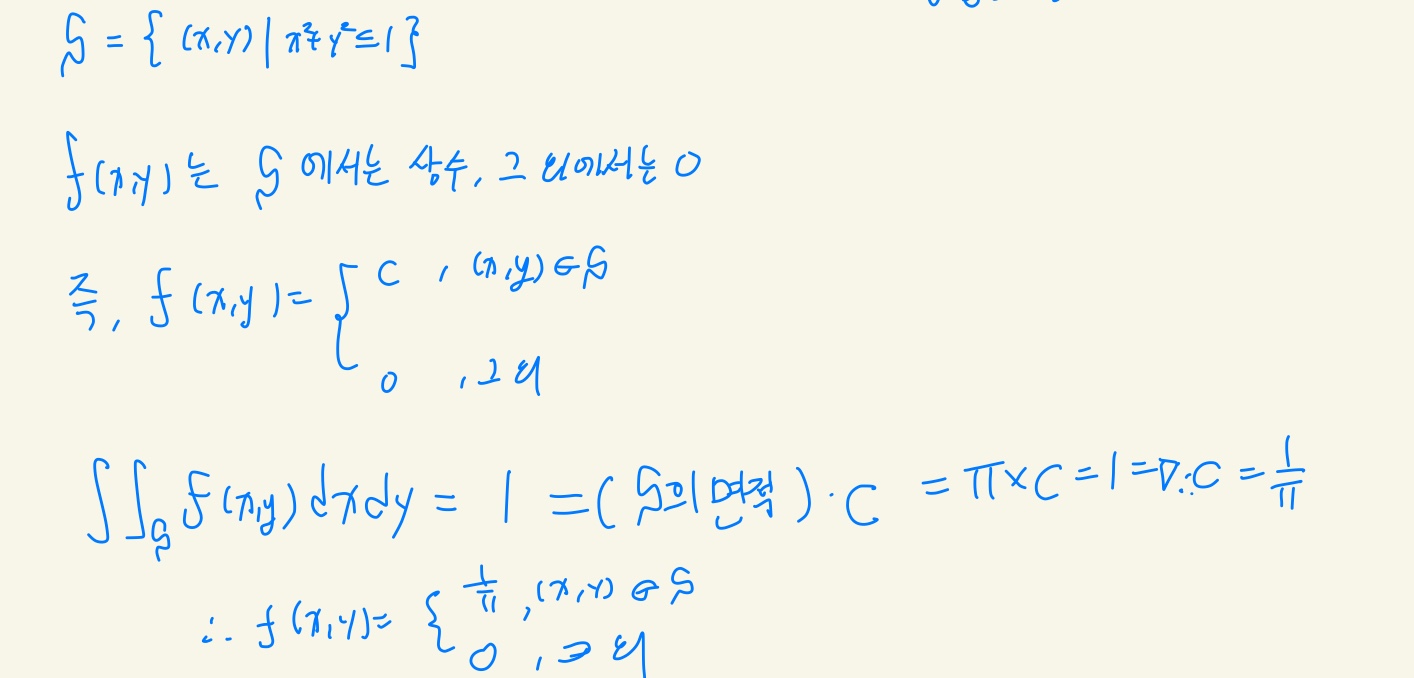
결합 분포 함수의 성질

'확률론 수업 정리' 카테고리의 다른 글
| 적률(moment) (0) | 2021.03.01 |
|---|---|
| 확률변수의 기댓값과 분산 (0) | 2020.08.11 |
| 분포함수 (0) | 2020.08.04 |
| 확률변수와 분포 (0) | 2020.08.04 |
| 독립사건 (0) | 2020.07.29 |


